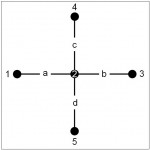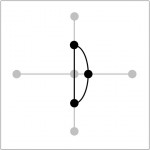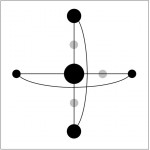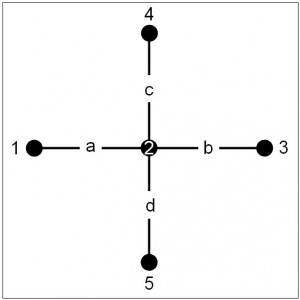
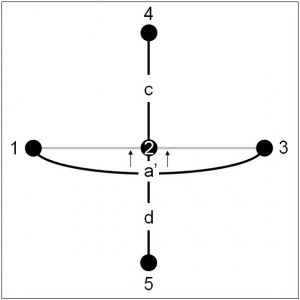
Figure 7.1: A Traditional Planar Graph-Street Network and a Space Syntax Representation
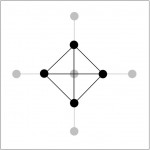
Figure 7.2: Dual and Primal Networks for the Two Map Problems
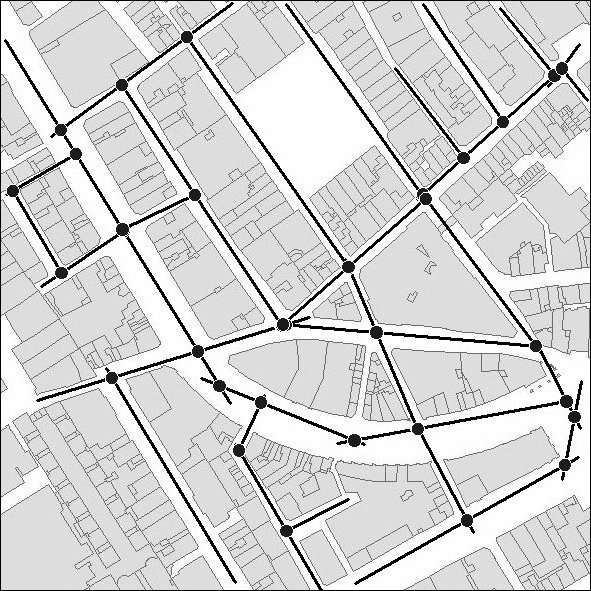
Figure 7.3: Axial Lines and Junctions in the Regent Street Area of Central London
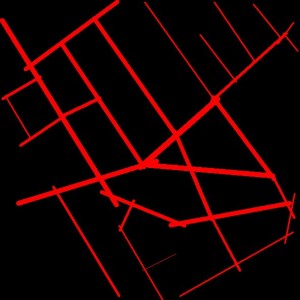
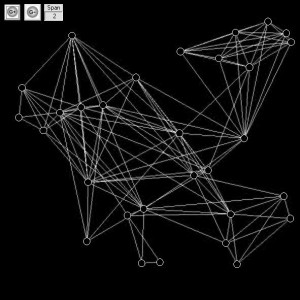
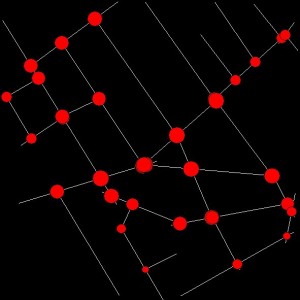
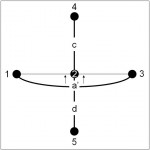
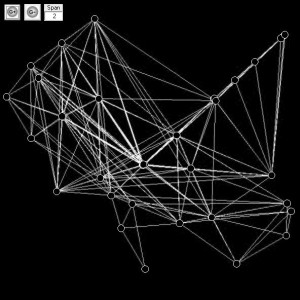Figure 7.4: Primal (a), (b) and Dual Networks (c), (d) Embedded In and Across Euclidean Space
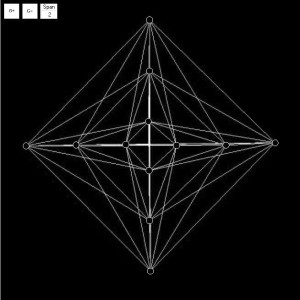
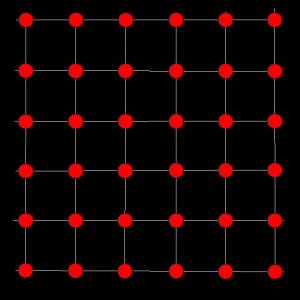
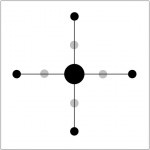
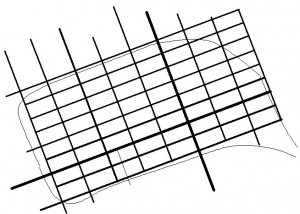
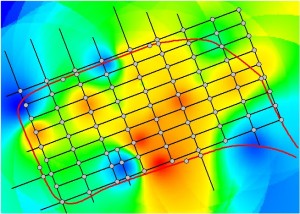
Figure 7.5: Space Syntax on the Manhattan Grid: Uniform Accessibilities
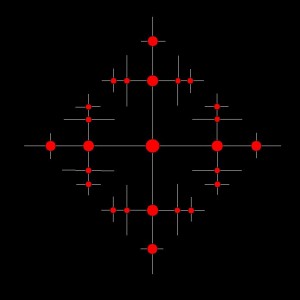
Figure 7.6: Space Syntax on a Fractal Tree: The Primal is the Dual
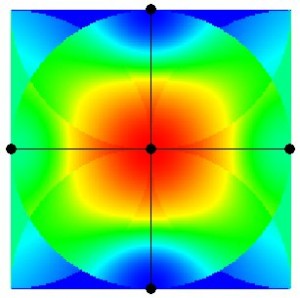
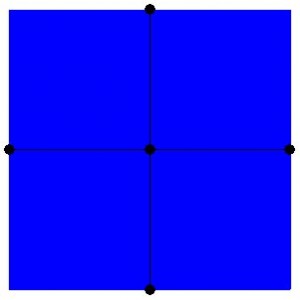
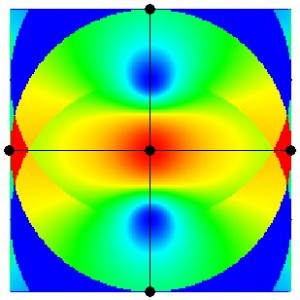Figure 7.7: Accessibility Surfaces for the Primal and Dual Problems from the Simple Planar and Axial Maps shown in Figures 7.1(a) and 7.1(b)
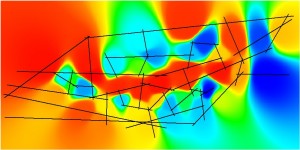
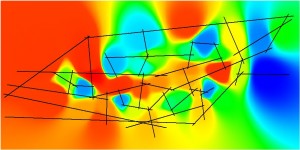
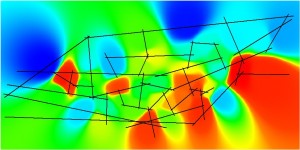
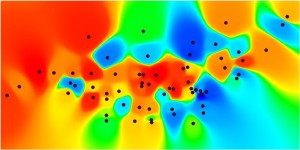
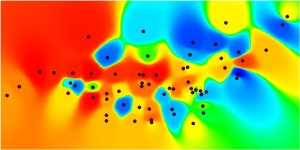
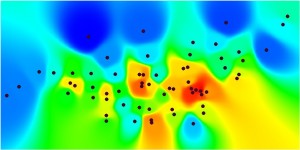Figure 7.8: Key Accessibility Measures for the Primal and Dual Pure Syntax Analysis of Gassin
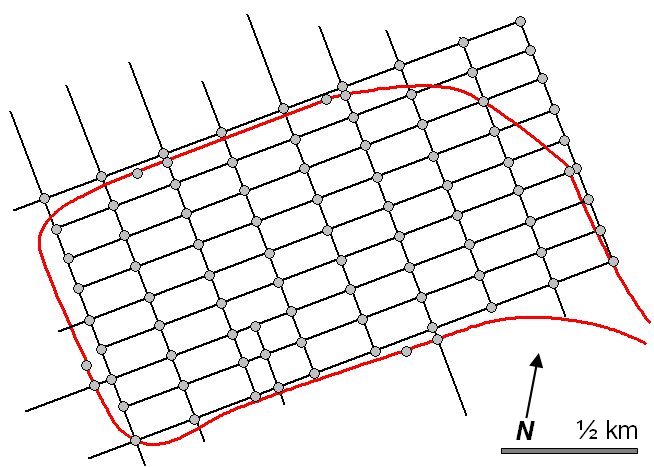Figure 7.9: The Street Grid for Central Melbourne with the Underground Rail Loop
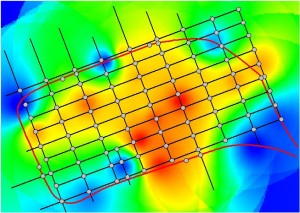
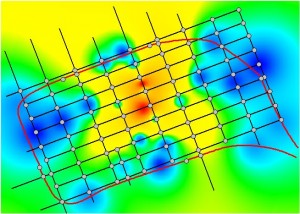Figure 7.10: Line Accessibility Surfaces Based on the Out-Degrees (a), Step-Distances (b), Weighted Distances (c), and Euclidean Distances (d)
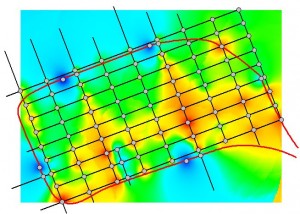
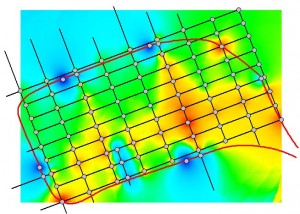
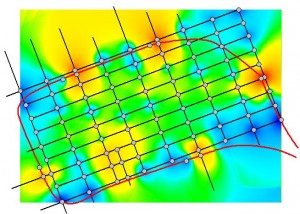Figure 7.11: Points Accessibility Surfaces Based on the Out-Degrees (a), Step-Distances (b), Weighted Distances (c), and Euclidean Distances (d)
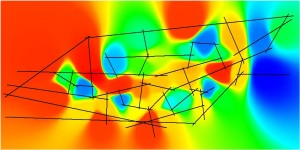
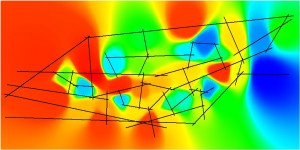
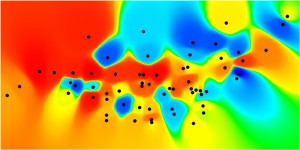
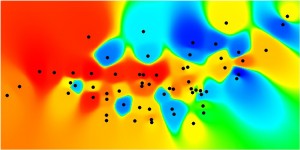Figure 7.12: Relative Proximities for the Primal and Dual Pure Syntax Analysis of Gassin
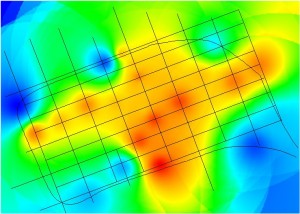
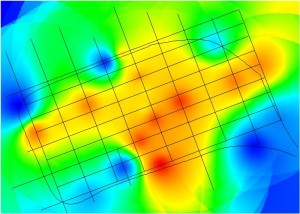
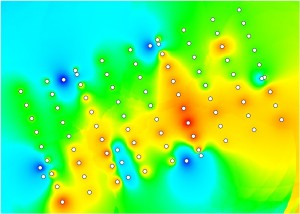
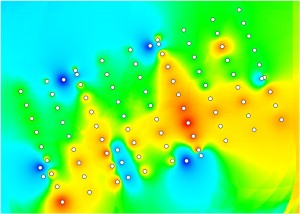Figure 7.13: Relative Proximities for the Primal and Dual Analysis of Central Melbourne
